Hierarchical clustering

Hierarchical clustering is an alternative approach to k-mean clustering algorithm for identifying groups in the dataset. It does not require to pre-specify the number of clusters to be generated. It uses pairwise distance matrix between observations as clustering criteria. Hierarchical clustering can be divided into two main types:

✓ Agglomerative clustering – It works in a bottom-up manner. Initially, each object is considered as a single-element cluster. At each step, the two clusters that are the most similar are combined together. This procedure is iterated until all points are member of just one single big cluster. The result is a tree which can be plotted as a dendrogram.

✓ Agglomerative clustering process:
(1) Start by assigning each item to a cluster, so that if you have N items, you now have N clusters, each containing just one item
(2) Then, compute the similarity distance between each of the clusters
(3) Join the two most similar clusters
(4) Repeat steps 2 and 3 until there is only a single cluster left

✓ An example of agglomerative clustering process is shown in Figure.

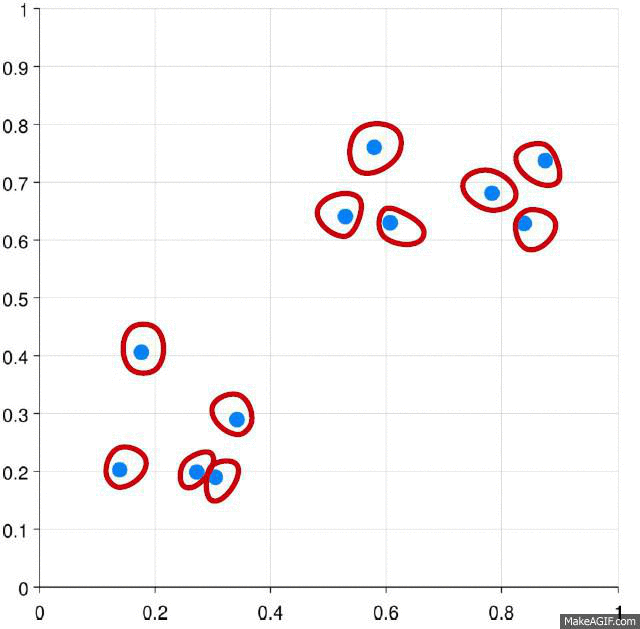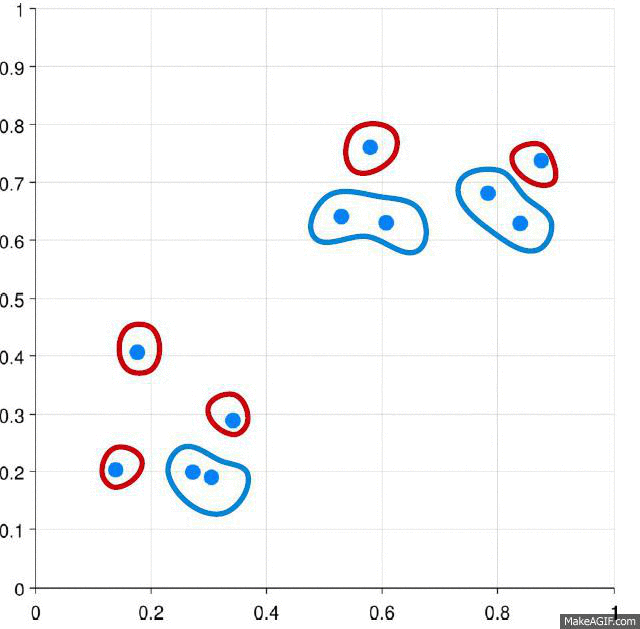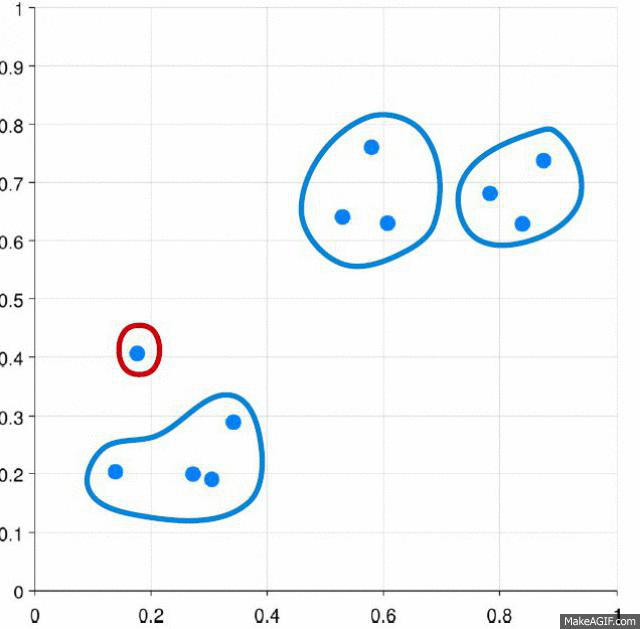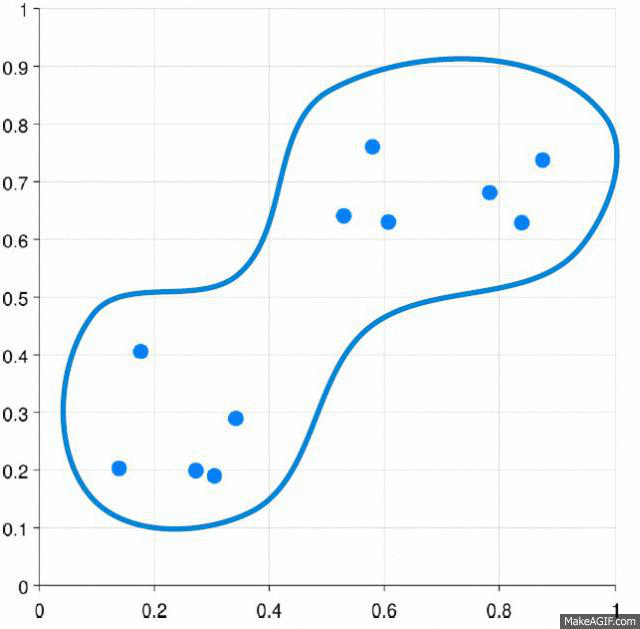
Different types of distance matrics such as Eculidean, Cosine, can be used estimate the distance between two clusters.

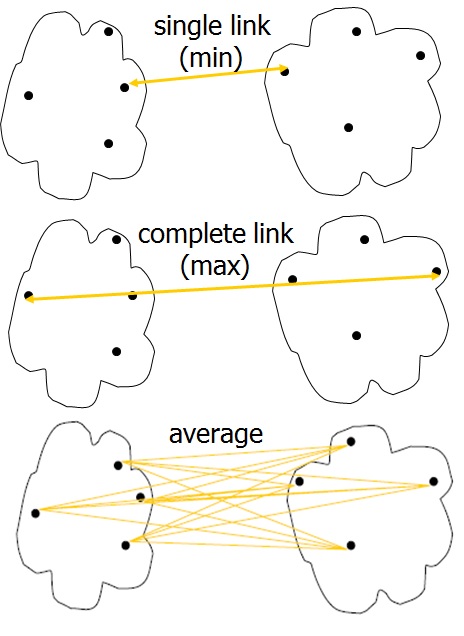
✓ Three methods are used to measue the distance between each cluster which is also shown in Figure:
(1) Single Linkage – The distance between two clusters is defined as the shortest distance between two points in each cluster.
(2) Complete Linkage – The distance between two clusters is defined as the longest distance between two points in each cluster.
(3) Average Linkage – The distance between two clusters is defined as the average distance between each point in one cluster to every point in the other cluster.

 

✓ Divisive hierarchical clustering – It works in a top-down manner. Intially, all the objects are included in a single cluster. At each step of iteration, the most heterogeneous cluster is divided into two. The process is iterated until all objects are in their own cluster.

✓ Strengths of Hierarchical Clustering
✶No assumptions on the number of clusters – Any desired number of clusters can be obtained by ‘cutting’ the dendogram at the proper level

✓ Complexity of hierarchical clustering.
✶Distance matrix is used for deciding which clusters to merge/split.
✶Not usable for large datasets.